최단 경로

1. 최단 경로

간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로를 최단 경로라고 한다.

가중치 모든 정점 경유 알고리즘
X O BFS
O X 다익스트라(단, 음의 가중치는 허용하지 않음), 벨만포드(음의 가중치 허용)
O O TSP, 순열(Back Tracking, DP)

2. 최단 경로 알고리즘

2-1. 다익스트라(Dijkstra) 알고리즘

시작 정점에서 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식이다.

시작 정점(s)에서 끝 정점(t)까지의 최단 경로에 정점 x가 존재한다. 이때, 최단경로는 s에서 x까지의 최단 경로와 x에서 t까지의 최단경로로 구성된다.(탐욕 기법을 사용한 알고리즘으로 MST의 프림 알고리즘과 유사함)

다익스트라를 사용하는 경우, 같은 최소 가중치를 가지는 경로가 여러개 존재할 수 있기 때문에, 최소 거리 경로를 묻기보다는 시작 점(s)과 끝 점(t)사이의 최소 가중치를 물어보는 경우가 대부분이다.

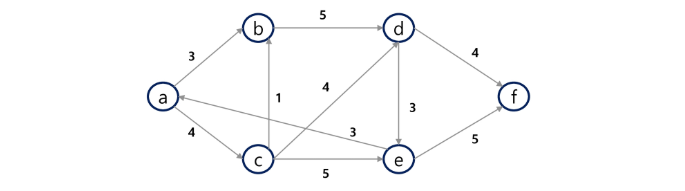
[예] 다음 그래프에 다익스트라를 적용하여 a에서 f까지의 최소 거리를 구하시오.

Dijkstra-Example

​ (답) 12

def dijkstra(s) :
​    visited[s] = 1
​    D = G[s]

    while 0 in visited :
        mini, w = 0, 0
        for i in range(len(D)) :
            if not visited[i] and (mini == 0 or D[i] < mini) :
                mini = D[i]
                w = i
        visited[w] = 1
        for i in range(len(D)) :
            D[i] = min(D[i], D[w]+G[w][i])
    return D[-1]


T = int(input())
for test_case in range(1,1+T):
​    N, E = map(int, input().split())
​    G = [[11]*(N+1) for _ in range(N+1)]
​    for _ in range(E) :
​        s, e, w = map(int, input().split())
​        G[s][e] = w
​    visited = [0]*(N+1)

    print('#{} {}'.format(test_case, dijkstra(0)))

3. 모든 쌍 최단 경로

모든 정점들에 대한 최단 거리를 구하는 방법

3-1. 플로이드- 워샬(Floyd-Warshall) 알고리즘

DP 기반의 알고리즘으로, 모든 점을 경유 가능한 점들로 고려하여 모든 쌍 i와 j의 최단 경로의 거리를 찾는 방식이다.

Floyd-Warshall

모든 정점에 대해 for문을 돌리는데 본인이 중간에 걸치거나, 시작정점이 아닐때만 조사한다. 이렇게 조사한 값과 바로 시작점에서 끝점까지의 값 중 최소 값을 반환하도록 한다.

'''
D[i][j]에는 선분 (i,j)의 가중치가 저장된다.
'''
allPairsShort(D) :
​    for k in range(1,n+1) :
​        for i in range(1,n+1) :
​            for j in range(1,n+1) :
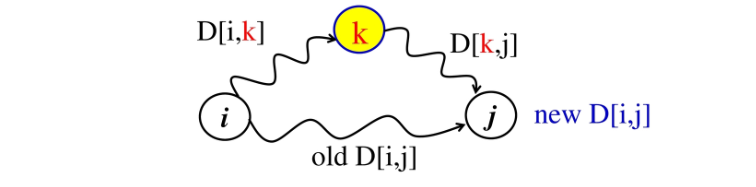
​                # i에서 j로 바로 가는 것과 i부터 k점까지의 최소 거리와 k부터 j까지의 최소거리의 합 중 작은 것이 i에서 j까지의 최단 경로이다. 
​				D[i][j] = min(D[i][k]+D[k][j], D[i][j])

(default)

(k=n+1)

루프를 다 돌고 나면 어떤 정점을 지났던 간에 i에서 j로 가는 가장 최소 가중치가 D[i].[j]에 저장된다.